Financial planning is a process, not a product so the saying goes. But what goes into the making of a financial plan? Of course there is a lot of uncertainty around the many twists and turns in this journey of life and your plan should adapt to that. But there is also a construct and there are some numbers that need to be crunched to have a good shot at the life you want to live.
So first a snapshot of the many goals you might have to plan for…

And with life after work (retirement) being the most expensive amongst them, we will use that as a use case to lay out the construct since the same process can be replicated for other life goals.
But before anything, a thing or two about perpetuities. Back in the day in 1751, the British government issued something called Consolidated Annuities or Consols that paid a fixed 3% rate of return each year (cash flows) and had no maturity date (cash flows go on forever).

The modern day equivalent of a Consol is a perpetuity as in the cash flows continuing forever.
And quite elegantly…
The present value (the price today if you were to buy it) of a perpetuity = C/r
C is the cash flow you receive each year if you were to buy this perpetuity and r is the interest rate or the rate of return.
Most long duration assets are perpetuities. Stocks, especially of the growth kind, in theory are the ultimate perpetuities because the present value of the cash flows that they’ll generate that’ll flow to you in the form of dividends twenty, thirty, fifty years down the road is very close to zero. And hence their valuation today can be condensed to a very simple perpetuity type model shown above.
So that was some necessary sidetrack but not to dwell on it much, the most important takeaway is the estimation of the present value of a perpetuity.
Back to planning for retirement, this is what the accumulation and the distribution phases look like for that goal.
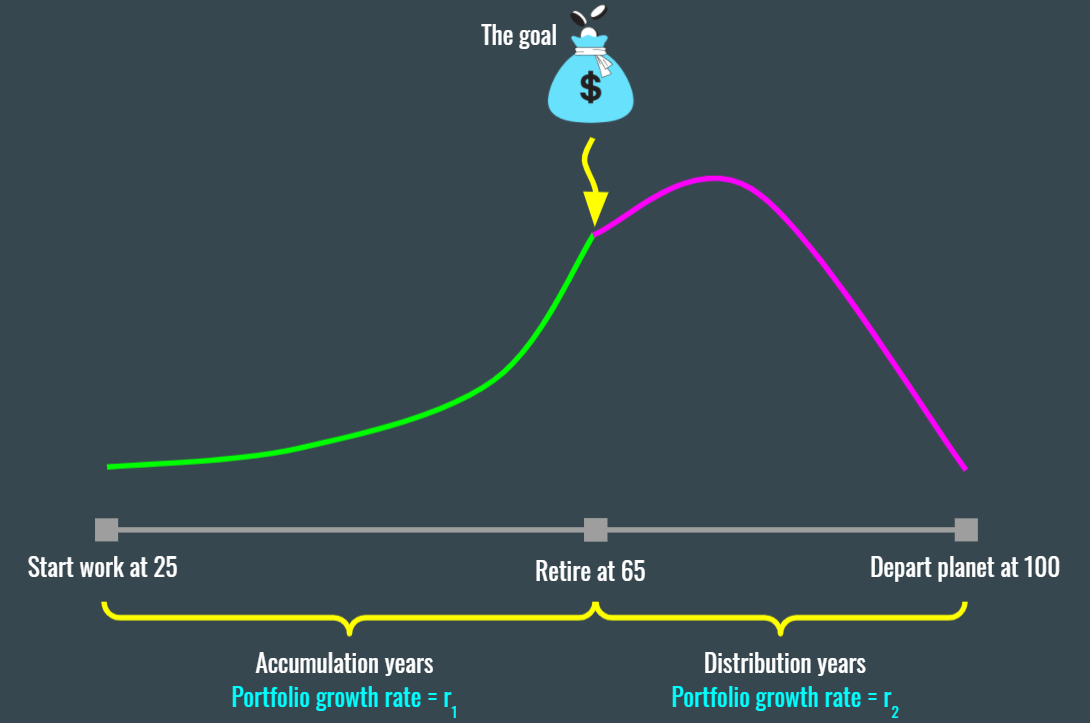
Though two different rates of returns are assumed for the two life phases, there is not and there should be not a clear demarcation between the two. Those rates of returns should change gradually, abruptly or none at all depending upon individual circumstances and market conditions but let’s assume these two distinct phases exist for you for now.
And we’ll start with the ‘in retirement’ phase first to help us quantify the $ value of the goal and then work backwards.

The first thing you’ll need to know are your income needs in retirement. I know it’s not easy to know that yet when you are like 25 but you should have some idea about the amount of money it takes to afford you a good life today. You then inflation adjust that to the year you retire and through retirement.
So during retirement, you’ll know the cash flow you’ll need and you have an estimate of the rate of return that the portfolio you’ll own is expected to deliver (r2 in this case).
Hence,
The $ value of the goal at retirement = The present value of a growing perpetuity that you buy right when you retire – The value of a growing perpetuity that you’ll buy at 100, discounted to the year you retire
Growing perpetuity is another flavor of a perpetuity where you assume growing cash flows (inflation-adjusted income need in retirement) instead of the constant cash flows we assumed in the original perpetuity equation.
So now that we know the $ value of the goal, we tackle the first phase of planning for retirement. And these are your accumulation years where you need to set aside a fixed amount of money each year to reach that goal.

We start with first discounting the $ value of the goal and bringing it to the present (at 25 in the plot above) using the assumed rate of return (portfolio growth rate = r1). Any savings (earmarked for retirement) that you already have now needs to be subtracted from the present value of the goal to calculate the gap you have to fill over the years to reach your goal.
That is…
The Gap = Present value of the goal – Savings you already have, earmarked for retirement
With this gap in savings required known, you can then reverse calculate the amount you need to set aside each year using the same perpetuity logic.
That is…
The Gap = The present value of a perpetuity you buy at 25 – The value of the perpetuity you buy at 65, discounted to the present (at 25)
You know the gap, you know the years to retirement and you know the portfolio growth rate during accumulation years and with that, you can back calculate the amount you need to save each year to fill that gap.
There is a lot that I skipped over to give a brief overview but for those interested in diving into the nitty-gritty of how this is done, a video tutorial is in the wings that I’ll release when ready.
Thank you for reading.
Cover image credit – Pixabay

