Wikipedia defines a polymath as an individual whose knowledge spans a substantial number of subjects and who is known to draw on complex bodies of knowledge to solve specific problems. Take Benjamin Franklin for example. Besides being one of our nation’s Founding Fathers, he was also a leading author of the time. Not only that, he was a scientist, an inventor, a postmaster, a printer, a humorist, a statesman, a diplomat…basically a polymath.
And we know that quote we still remember him by, “A penny saved is a penny earned.” But he is also known for another quote that describes the process of compounding as best as one can. That quote, “Money makes money, and the money that money makes, makes money.”
He died in 1790 and bequeathed his life savings, a cool $10,000 (of that time so big money then) to be equally split between two of his favorite cities, Boston and Philadelphia but with a condition. The first half of that money should be invested and should remain invested and can only be used after 100 years. The second half needs to remain invested and can only be spent after 200 years.
And that’s what the cities did. In 1890, at the end of the first 100 year period, both cities used $500,000 each to be spent on public goods. That’s what 100 years of compounding $2,500 that each city received does. The calculated rate of return to turn $2,500 into $500,000 after 100 years ~ 5.44%. So very ordinary.
And here are the numbers over time…
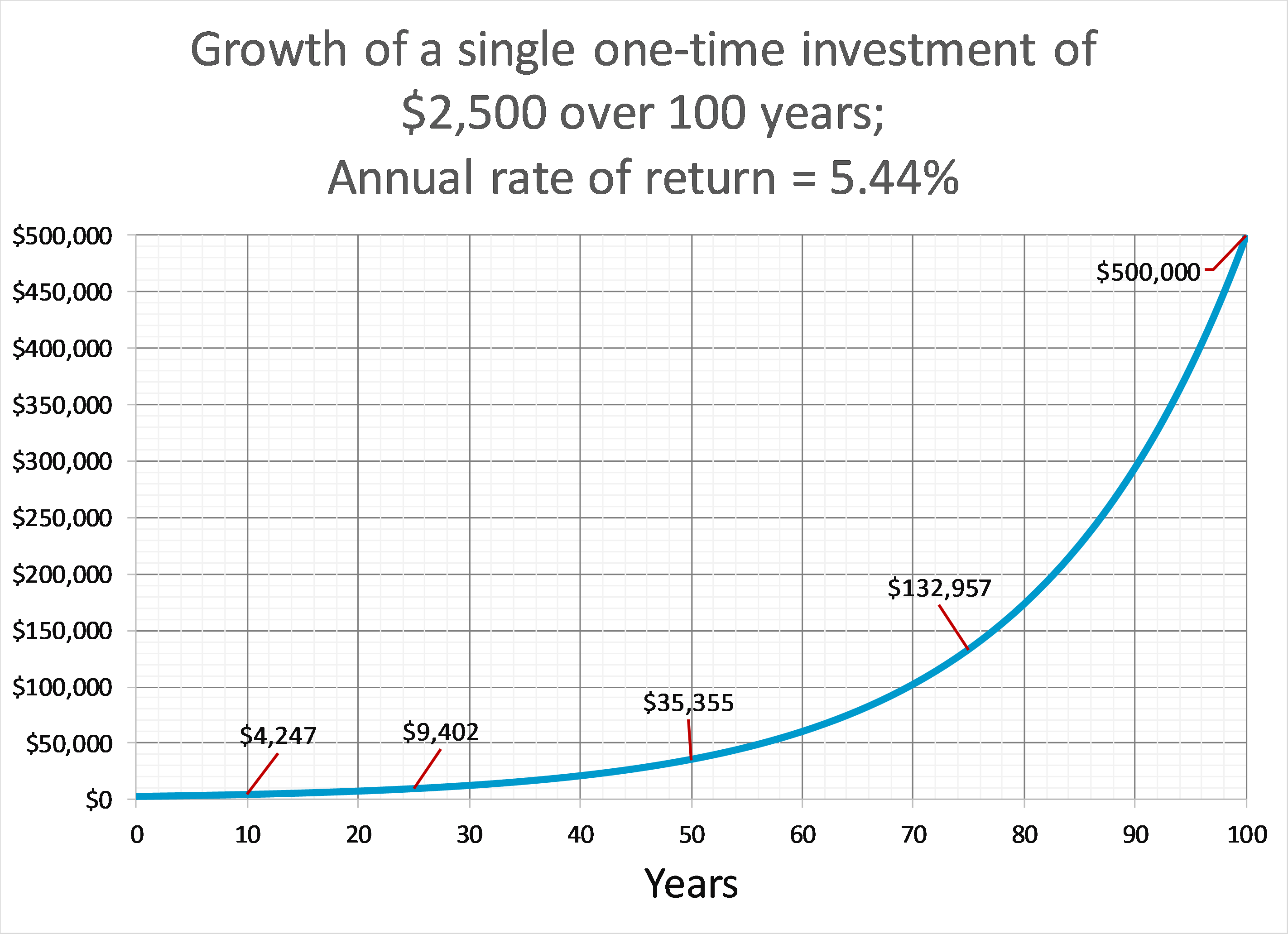
So that was the first 100 years.
In 1990, both cities got access to the rest of the money. Any guesses on how much the other half grew to? How about 20 million bucks and that’s for each city. So that’s 200 years of compounding the remaining $2,500 that was bequeathed to each city.
And the annual rate of return required to turn that ‘tiny’ sum to 20 million bucks? 4.6%. Again, pretty average. In fact, that’s below average historically and yet the result, extraordinary.
And when you are dealing with 200 years of compounding, a tiny change in the rate of return makes a big difference in what you get at the other end. Go ahead, pull out that spreadsheet and give it a try.
So time truly is magical. But the first step to compounding is to have something saved to compound. You could be the greatest investor who ever lived but zero dollars will still be zero dollars regardless of the rate of return. So save.
And to find out how much your savings will grow to at some future date, you can use this little bit and the only bit of math here and ever.
FV = PV (1 + r)t
FV is the Future Value of your savings
PV is the Present Value
r is the rate of return
t is time
I love playing around with this by trying out different values for the rate of return and time. Let’s try one. Say I had 100 dollars (PV) saved and I bought an investment with an annual rate of return of 6% (r) and I invested that money for say 5 years (t), I’d have a total of $134 at the end of that 5 year period. Just plug the numbers into the equation and solve for whatever you are trying to find out. In this case, we want to find FV like below.
FV = $100 (1 + 0.06)5
But compound interest is slow and boring…at least at the start.
And here’s what I mean. Say you are 20 and you start setting aside $500 each month and invest that at an 8% rate of return each year and you do that for 45 years (till you are 65), this is what you’ll have…
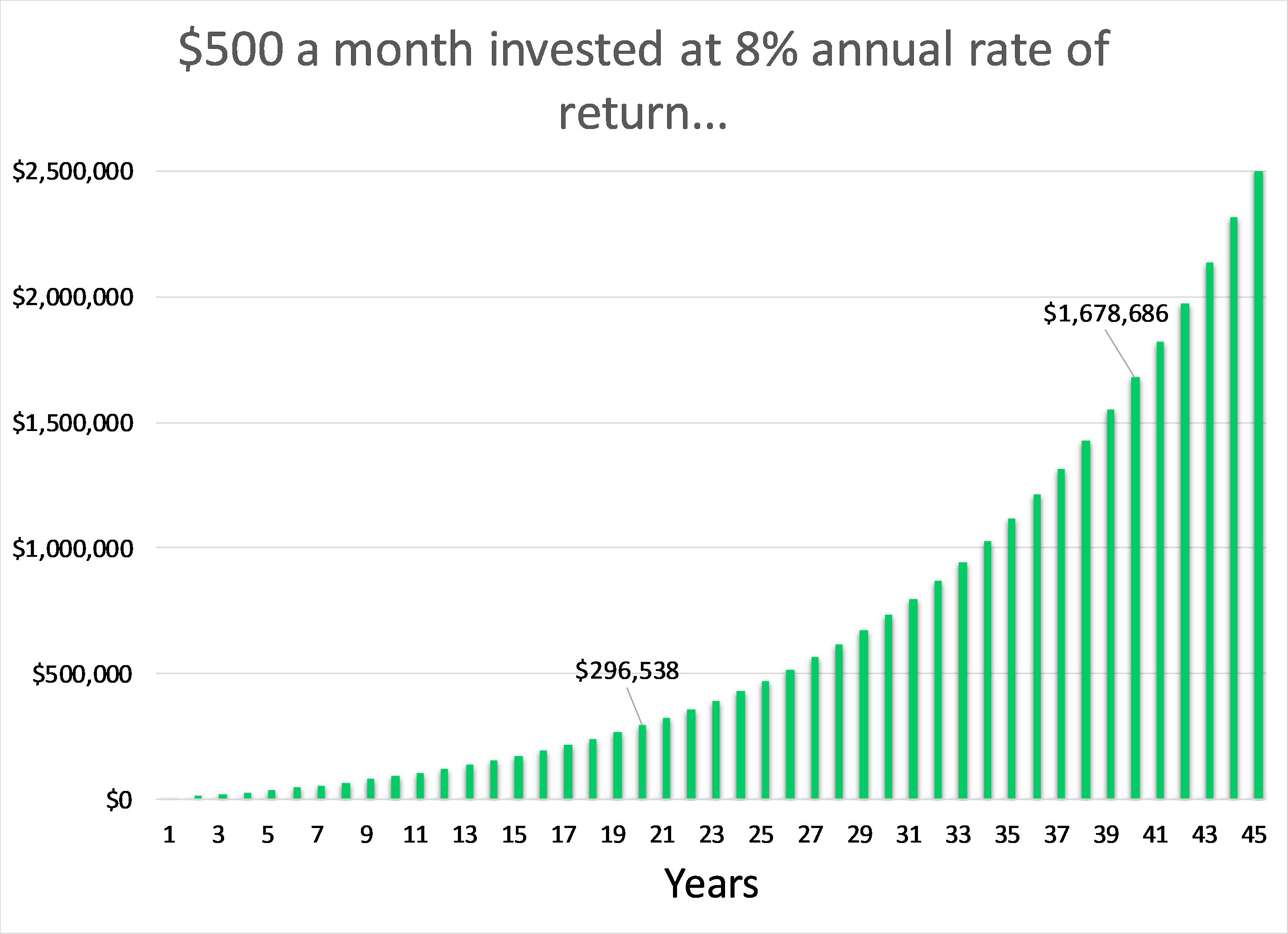
But just look at these numbers…
- 20 years in, you invested $120,000 and you earned $176,538. Big deal but then, no big deal.
- 40 years in though, you invested a total of $240,000 but you earned $1,438,686. Now that’s something.
This compounding thingy really starts to become fun only after a couple decades.
Here’s another more fun example. Say at 15, I start a business and I clear $3,000 in profits that year and I do that for 5 years. Now a saver that I am, I don’t spend nothing all those years so at the end of five years of toiling, I accumulate $15,000 in total. And say that’s all the savings I’ll do through my life. Not likely but let’s assume that. And I don’t need the money because I get to live and eat and have fun for free (how? that’s a secret). So then what do I do? I go to my dad to ask for advice and since I don’t need the money for a long, long time, he recommends investing the entire amount in a global portfolio of stocks.
My sister on the other hand, in her attempt at imitating me, does the same exact thing. She starts a business when she turns 15 generating the same amount of profits each year. But a spendthrift that she is, she spends it all. At 25, she gets to have a peek at my account and she realizes that she is falling behind in terms of all this savings thingy so she starts and continues saving till she is a grand old lady at 65.
And like me, she also seeks advice from our dad on where and how to invest her savings and THE dad that he is, recommends the exact same portfolio. I started 10 years earlier and I saved and invested only $15,000. My sister started 10 years later but she saved and continued investing till she reached 65. So she invested a total of $120,000 (40 years x $3,000 each year). Who wins? Of course I do.
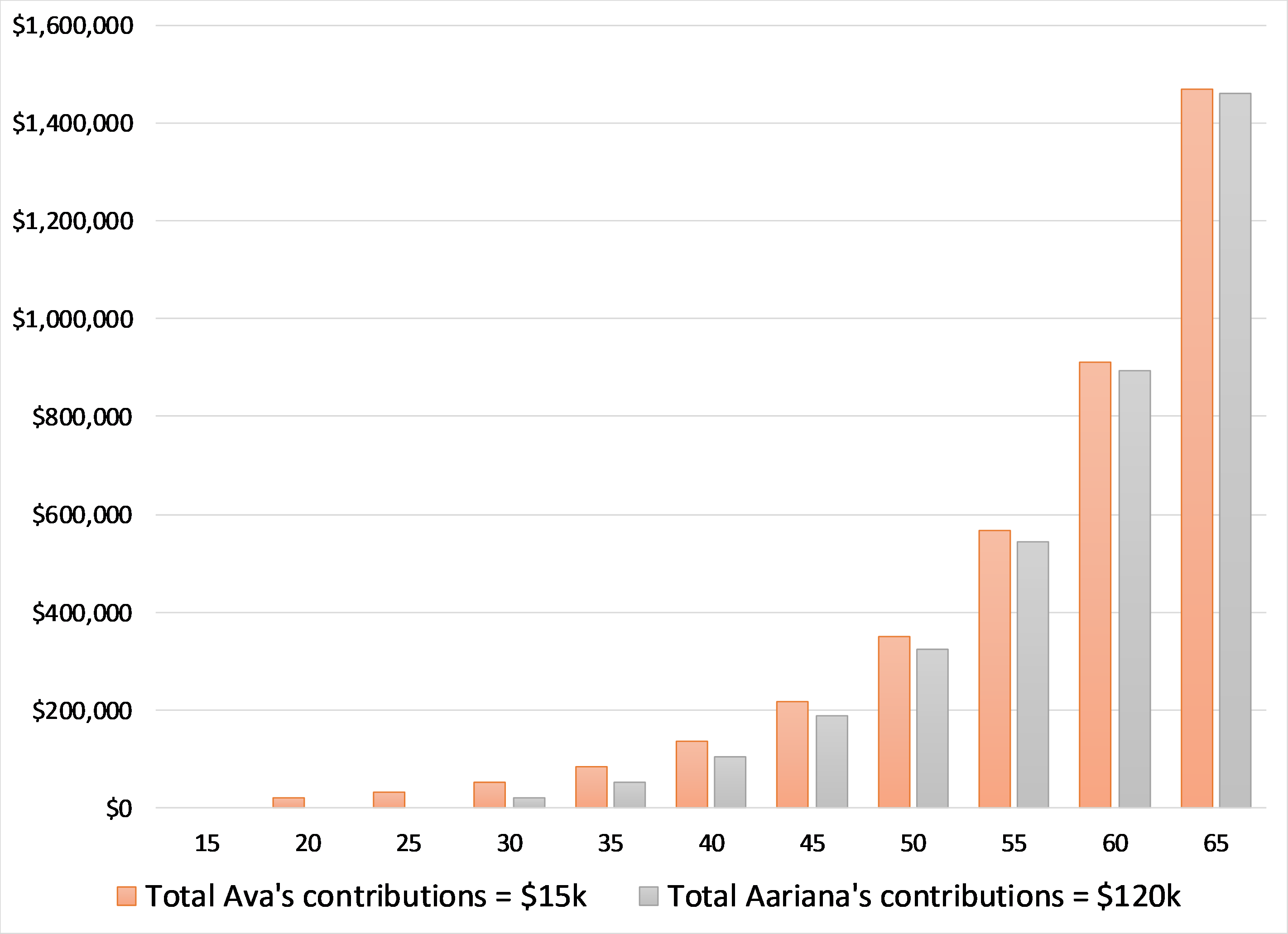
Because I got a 10 year headstart, my little sis could never catch up with me even after saving 6x more. That’s the secret I was talking about.
Thank you for reading.
Bye.
Cover image credit – iheitlager, Flickr

